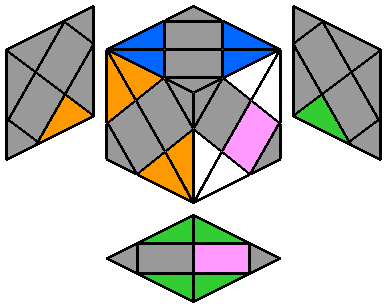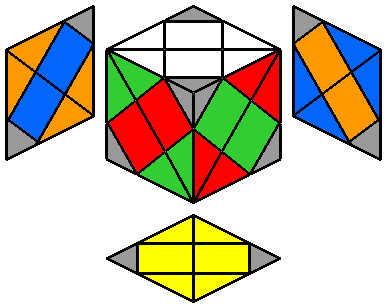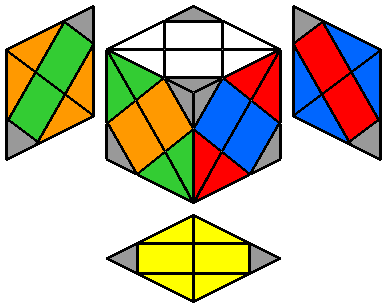|
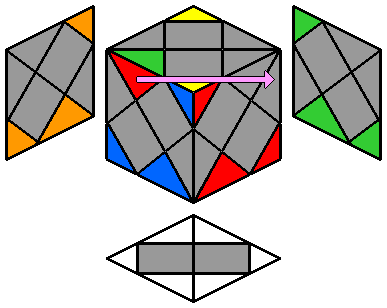
Comme son nom l'indique, le Dino Skewb est un hydride entre un Dino et un Skewb. C'est à dire que, sur ses 8 coins, 4 tournent comme un Dino et 4 comme un Skewb.
C'est un cube déroutant, car je l'imaginais facile comme le sont le Dino et le Skewb. Mais entre les mains, il s'avère particulièrement difficile et ne répond ni à la logique ni aux algorithmes du Dino et du Skewb. Il faut dont le repenser totalement et le considérer indépendamment de ses 2 précurseurs.
Le Dino Skewb se compose de 3 sortes de pièces : les centres (qui n'ont qu'une couleur), les arêtes (à 2 couleurs) et les coins (à 3 couleurs). En essayant d'adapter et combiner les formules classiques du Dino ou du Skewb, on se rend compte que les pièces les plus difficiles à placer sans déplacer les autres sont les arêtes. Par conséquent, la stratégie que j'utilise pour reconstruire ce cube consiste à repositionner les arêtes en premier, puis les centres et enfin les coins.
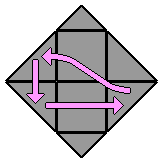
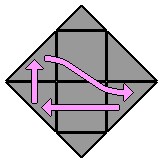
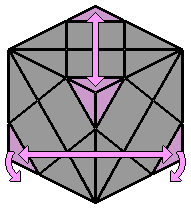
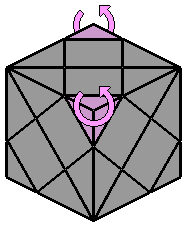
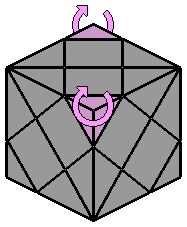
La notation conventionnelle que je propose ici est un peu différente, puisque l'observateur se place face au coin qui est dans l'alignement des 2 centres de la face du dessus. Seuls quelques mouvements sont nécessaires pour expliciter les algorithmes de résolution présentés plus bas :
|
|
|
|
= R
Ce mouvement correspond à une rotation d'un tiers de tour dans le sens horaire du coin droit (right).
Si la rotation se fait dans le sens inverse, je noterai R'. |
|
|
|
|
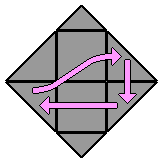
= L
Ce mouvement correspond à une rotation d'un tiers de tour dans le sens horaire du coin gauche (left).
Si la rotation se fait dans le sens inverse, je noterai L'. |
|
|
|
|
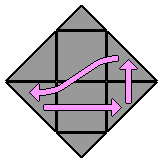
= F
Ce mouvement correspond à une rotation d'un tiers de tour dans le sens horaire du coin avant (front).
Si la rotation se fait dans le sens inverse, je noterai F'. |
|
|
|
|
= f
Ce mouvement correspond à une rotation d'un tiers de tour dans le sens horaire du coin avant et de sa 2ème couronne (front).
Si la rotation se fait dans le sens inverse, je noterai f'. |
|
|
|
|
= D
Ce mouvement correspond à une rotation d'un tiers de tour dans le sens horaire du coin inférieur (down).
Si la rotation se fait dans le sens inverse, je noterai D'. |
|
|
|
|
= G
Ce mouvement correspond à une rotation d'un tiers de tour dans le sens horaire du coin inférieur droit.
Si la rotation se fait dans le sens inverse, je noterai G'. |
|
|
|
|
|
|
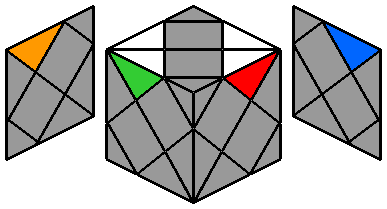
1. Placer les arêtes blanches :
|
|
|
Je commence par positionner les 4 arêtes blanches à la face supérieure, une par une dans le sens des aiguilles d'une montre.
Il n'y a pas de méthode particulière à cette étape, il s'agit de déplacements simples et familiers au Dino et au Skewb.
La seule difficulté est de penser à la correspondance des couleurs. Mais la disposition est la même que celle des autres cubes habituels, bleu-rouge-vert-orange.
La finalité de cette étape est donc d'obtenir la configuration ci-contre à droite.
|
|
 |
|
|
|
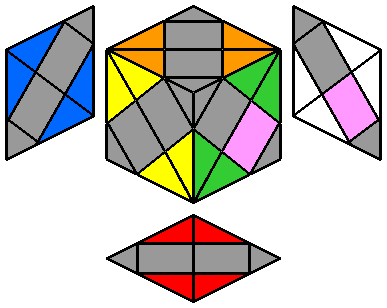
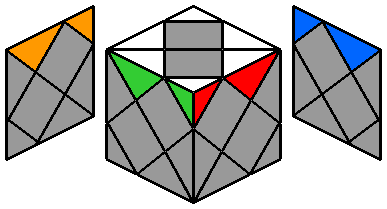
2. Placer les coins blancs :
|
|
|
Puis je positionne les 2 coins blancs à la face supérieure.
C'est la même façon de faire que pour placer les coins blancs à la première étape de résolution du Skewb.
C'est facile. |
|
 |
|
|
|
3. Placer les coins jaunes :
|
|
|
Ensuite, je retourne le cube de 180° pour que la future face jaune regarde vers le haut.
Par simple rotation, j'oriente la couleur jaune de chacun des 2 coins vers le haut (2 mouvements au maximum sont utiles).
J'obtiens donc la configuration ci-contre à droite, où les 4 arêtes blanches et les 4 coins sont bien placés. Je vais pouvoir maintenant positionner les dernières arêtes.
On pourrait croire que cette étape de positionnement des 4 coins est inutile à ce stade, d'autant que par la suite, lorsqu'on va placer les autres arêtes et les centres, ces 4 coins vont se déplacer. Mais en réalité, c'est une phase cruciale pour éviter les problèmes de parité en fin de résolution.
Si on ne la respecte pas, on se retrouvera à coup sûr avec un coin solitaire qui refuse de s'aligner avec les autres. |
|
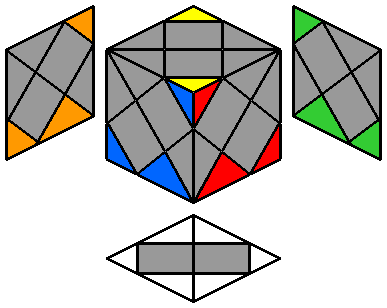 |
|
|
|
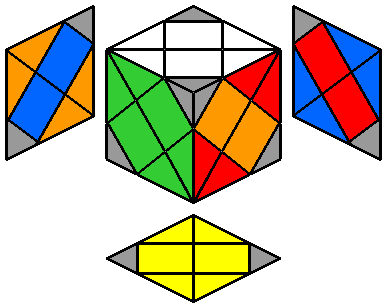
4. Placer les dernières arêtes :
Pour positionner les dernières arêtes sans perdre la parité des coins, j'utilise un algorithme qui échange 3 arêtes de la face supérieure. Le voici illustré ci-dessous avec ses effets suivant ses variantes miroir (vues supérieures) :
|
|
|
|
|
|
L F' L' F (n°1) |
F' L F L' (n°2) |
R' F R F' (n°3) |
F R' F' R (n°4) |
|
|
|
Je commence toujours par positionner les arêtes des faces latérales, c'est à dire celles qui ne contiennent ni blanc ni jaune. Je cherche donc en premier lieu une arête de la face supérieure qui n'ait pas de jaune. Je repère ensuite l'endroit où doit aller cette arête et je pivote un des 4 coins de la face supérieure pour que ces 2 arêtes en question (l'arête non jaune et l'arête de sa position finale) se retrouvent à la face supérieure. Puis j'applique un des 4 algorithmes ci-dessus et je repositionne le coin que j'ai tourné à sa position initiale.
Je n'ai plus qu'à excuter la même chose pour les 3 autres arêtes des faces latérales et toutes les arêtes non jaunes seront bien positionnées.
Si, mal malchance, les arêtes latérales ne sont pas correctement positionnées, mais qu'il y a que des arêtes jaunes à la face supérieure, alors je fais un coup pour rien en descendant une arête jaune quelconque pour la repositionner plus tard, exactement comme pour les arêtes de la 2ème couronne du 3x3x3.
Prenons deux exemples concrets :
|
|
|
|
Dans l'exemple ci contre à gauche, il y a une arête non jaune à la face supérieure : l'arête bleue-rouge. Celle-ci doit venir se placer un peu plus bas entre les arêtes blanc-bleu et blanc-rouge. On serait dont tenté de faire tout simplement F' et l'arête serait bien positionnée. Mais dans ce cas, j'aurais modifié la parité du coin jaune avant (par rapport au coin jaune arrière) et je ne pourrai jamais résoudre les coins à la dernière étape.
Pour placer cette arête bleu-rouge,
je vais tourner le coin avant (F) pour que cette arête bleu-rouge et l'arête de sa future position se retrouvent à la face supérieure. Ensuite, je choisis l'algorithme qui amènera l'arête bleu-rouge (maintenant sur la droite) au niveau de l'arête avant gauche, c'est à dire l'algorithme n°2 ou n°3, au choix. Puis je replace le coin avant pour conserver la parité (F').
Ce qui nous donne si on choisit l'algorithme n°3 : F [R' F R F'] F'
L'arête bleu-rouge est désormais bien placée. Notez que les coins jaunes ont pivoté dans cette affaire, mais ils ont pivoté ensemble et conservent donc leur parité. |
|
|
|
Notez également que si j'avais choisi l'algorithme n°2, cela aurait donné la formule F [F' L F L'] F' qui se simplifie en L F L' F', ce qui est une variante des 4 algorithmes de référence et qui permet d'échanger 3 arêtes à la partie gauche du cube en incluant une arête latérale. Personnellement je n'encombre pas ma mémoire avec ces variantes peu utiles et ne retiens que les formes qui déplacent les arêtes supérieures. L'économie n'est pas suffisamment rentable à mon sens. Mais chacun est libre d'apprendre autant de formules qu'il le souhaite.
|
|
|
|
Deuxième exemple, ci contre à gauche, l'arête non jaune à placer est maintenant la rouge-vert, qui doit aller vers la droite.
Pour placer l'arête de destination à la face supérieure, j'ai 2 éventualités :
- soit je fais R', l'arête de destination est désormais en haut à droite de la face supérieure et pour y déplacer l'arête rouge-vert, je devrai utiliser l'algorithme n°3.
- soit je fais R, dans ce cas, l'arête de destination est en bas à droite sur la face supérieure. Je devrai alors utiliser l'agorithme n°1 ou le n°4 pour amener l'arête rouge-vert sur la droite.
J'ai donc 3 solutions possibles :
- R' [R' F R F'] R ;
- R [L F' L' F] R' ;
- R [F R' F' R] R' (= R F R' F', je ne reviens pas sur les variantes des 4 algorithmes intéressant les arêtes latérales).
Notez que là aussi, 2 coins ont été pivotés sur eux-mêmes, cette fois-ci c'est un jaune et un blanc, mais toujours symétriquement, et donc avec une parité respectée.
|
|
|
|
Une fois que les 4 arêtes latérales sont placées, il ne reste plus que des arêtes jaunes à la face supérieure, qu'on va correctement positionner avec un (voire 2) des 4 algorithmes de base ci-dessus.
5. Regrouper les centres de même couleur :
Les arêtes sont donc toutes en place, nous allons maintenant
reconstruire les centres. Pour cela, je commence par réunir 2 par 2 les centres de même couleur, peu importe la face sur laquelle ils sont. Ensuite, quand les 6 groupes de centres sont formés, je les réorganise sur leurs bonnes faces.
Trois outils à connaître :
|
|
|
| |
5.1. |
|
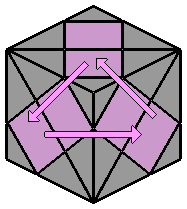
= R L' R' L
Pour la recontruction des centres, j'utilise comme base cet algorithme simple qui permet d'échanger 3 groupes de 2 centres.
Le groupe en bas à droite monte. Celui du haut descend en bas à gauche. Et celui en bas à gauche reste en bas mais va sur la droite. Il faut savoir qu'au sein d'un groupe de 2 centres, le centre qui est en haut reste toujours en haut lors de ces déplacements. Ce qui signifie que les groupes qui montent ou qui descendent se déplacent par simple translation. Mais le groupe qui reste en bas se déplace par symétrie d'axe vertical. |
|
|
|
| |
5.2. |
|
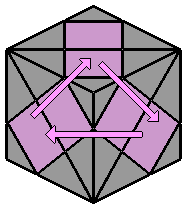
= L' R L R'
La forme miroir permet la même rotation dans le sens inverse. |
|
|
|
| |
5.3. |
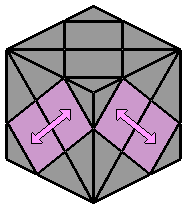
|
= [R L' R' L] [D' L D L']
Sur le principe que certains groupes se déplacent par translation et d'autres par symétrie, si on utilise 2 fois l'algorithme [5.1] avec une orientation différente, on peut échanger les centres de 2 groupes. |
|
|
|
|
Pour réunir 2 centres sur la même face, on va devoir rapprocher ces 2 centres sur 2 faces adjacentes, uniquement séparés par un coin, comme dans l'illustration à gauche. On se servira pour cela des 3 algorithmes ci-dessus.
Alors, on remplace un centre par son jumeau par rotation d'un coin. Puis on échange ce centre par l'algorithme [5.3], et on replace le coin qu'on a pivoté initialement.
Ce qui donne en pratique à travers 2 exemples (mais qui sont équivalents) :
|
|
|
|
|
|
|
G [R L' R' L D' L D L'] G' |
G' [R L' R' L D' L D L'] G |
|
|
|
On réunira ainsi l'un après l'autre les 6 groupes de centres. Lorsque ceux-ci seront tous appairés, on va pouvoir les positionner sur leurs bonnes faces.
6. Placer les centres :
Tout d'abord, je place correctement les centres de 2 faces opposées avec les algorithmes [5.1] et [5.2]. Puis, j'oriente le cube afin que ces faces soient en haut et en bas (faces blanche et jaune dans les exemples ci-dessous) et j'observe ce qui se passe.
|
|
|
| |
6.1. |
|
Premier cas de figure : il y a déjà un centre bien positionné sur les faces latérales (le vert dans l'exemple ci-contre). Je tourne le cube pour qu'il soit à l'avant. Il sera dans ce cas sur la gauche (pour que la face supérieure garde sa bonne orientation). Les autres centres doivent alors tourner dans le sens horaire (vus de dessus).
Je fais : [5.1] + [5.2 sur la face arrière] + [5.2 à nouveau sur la face avant]. C'est à dire :
[R L' R' L] [R' L R L'] [L' R L R']
Les centres sont tous bien placés !
Cette succession d'algorithmes est plus simple qu'il n'y paraît. En pratique, je place le centre latéral correct à l'avant, pour que la face supérieure soit orientée convenablement, donc sur la gauche dans cet exemple. Par conséquent, je commence l'algorithme par la droite ([5.1]). Puis je pivote le cube pour basculer sur l'arrière, et pour replacer 2 centres sur 3, je vois que je dois faire [5.2]. Enfin, je repasse à l'avant et je vois qu'il n'y a qu'à faire [5.2] pour que tous les centres soient bons. Finalement, il suffit de regarder, pas besoin d'apprendre quoi que soit bêtement. |
|
|
|
| |
6.2. |
|
Deuxième cas de figure : le centre bien placé est toujours à l'avant gauche et les autres centres doivent tourner dans le sens anti-horaire (vus de dessus).
Je fais : [5.1 face avant] + [5.1 face arrière] + [5.2 face avant]
[R L' R' L] [L R' L' R] [L' R L R'] |
|
|
|
| |
6.3. |
|
Troisième cas : le centre bien placé est à l'avant droite et les autres centres doivent tourner dans le sens anti-horaire (vus de dessus).
Je fais : [5.2 face avant] + [5.1 face arrière] + [5.1 face avant]
[L' R L R'] [L R' L' R] [R L' R' L] |
| |
6.4. |
|
Quatrième cas : le centre bien placé est à l'avant droite et les autres centres doivent tourner dans le sens horaire (vus de dessus).
Je fais : [5.2 face avant] + [5.2 face arrière] + [5.1 face avant]
[L' R L R'] [R' L R L'] [R L' R' L] |
| |
6.5. |
|
Cinquième cas : les centres opposées doivent être échangés.
Je fais : [6.2] + [6.3]... ce qui se simplifie en :
[5.1 face avant] + [5.1 face arrière] + [5.1 face avant] + [5.1 face arrière] + [5.1 face avant] |
| |
6.6 |
|
Sixième cas : 2 centres adjacents (de face) doivent être échangés.
Je fais : [6.2] + [6.3 face arrière]... ce qui se simplifie en :
[5.1 face avant] + [5.1 face arrière] + [5.2 face avant] + [5.2 face arrière] + [5.1 face avant] + [5.1 face arrière] |
| |
6.7 |
|
Dernier cas : 2 centres adjacents (de côté) doivent être échangés.
Je fais : [6.1] + [6.4]... ce qui se simplifie en :
[5.1 face avant] + [5.2 face arrière] + [5.1 face avant] + [5.2 face arrière] + [5.1 face avant] |
|
|
|
7. Recontruire les coins :
Il ne reste plus qu'une dernière étape : positionner et orienter les coins.
On piochera parmi les 3 algorithmes ci-dessous celui ou ceux dont on a besoin :
|
|
|
| |
7.1. |
|
= [R L' R' L] [R L' R' L] [R L' R' L]
En appliquant 3 fois d'affilée l'algorithme [5.1], on va échanger, deux à deux, les coins supérieurs et les coins inférieurs.
Dans leur déplacement, les coins supérieurs garderont la même face orientée vers le haut. En revanche, les coins inférieurs pivoteront. On choisira donc judicieusement comment appliquer cet algorithme pour économiser d'autres déplacements inutiles. |
|
|
|
| |
7.2. |
|
= [R L' R' L] f [L' R L R'] f'
On peut corriger l'orientation des 2 coins supérieurs avec cet algorithme.
Ceux qui n'ont pas
envie d'apprendre une nouvelle formule pourront aussi faire [7.1] F [7.1] F', mais c'est plus long...
|
|
|
|
| |
7.3. |
|
= [R L' R' L] f' [L' R L R'] f
La forme miroir du précédent, dont l'équivalent sera [7.1] F' [7.1] F. Mais on peut tout aussi utiliser le cas [7.2] sur la face arrière, pour le même résultat. |
|
|
|
| Et c'est terminé ! |
 |
|
|
|
Avec cette méthode, je mets environ 2 minutes pour reconstruire ce cube.
|
|
|
Quelques photos souvenirs :
|
|
|
 |
|
DaYan Dino Skewb (Stickerless) de 2016. |
|
 |
|
 |
|
Une construction à la française. |
|
|
|