|
Pour résoudre le cube 6x6x6, j'utilise la même méthode que pour le 4x4x4 ou le 5x5x5. Toutes les techniques à connaître ont déjà été vues dans ces dernières pages. Il n'y a que quelques variantes qu'on va passer en revue... |
|
|
Je rappelle la notation conventionnelle que j'utilise ici :
|
 |
|
|
|
|
|
|
1. Refaire les centres :
Je commence, comme pour le 4x4 et le 5x5, par reconstruire les centres de chaque face, un par un. Il n'y a pas de difficulté particulière pour les premiers centres. Je forme une ligne verticale de 1x4 sur la face antérieure, puis je la monte, en faisant attention de ne pas défaire les autres centres déjà construits. Ligne après ligne, sans ordre particulier puisqu'il n'y a pas de petit cube central sur ce cube pair, chaque centre est reconstitué, blanc, jaune, bleu, orange.
Pour les 2 derniers centres, j'échange un maximum de cubes rouges et verts (les lignes avec 3 ou 4 cubes de couleur opposée) et je replace les derniers restants à l'aide des algorithmes suivants :
|
|
|
|
|
|
| |
L1' U R1 U' L1 U R1' |
L2' U R1 U' L2 U R1' |
L1' U R2 U' L1 U R2' |
|
|
|
|
|
|
|
|
|
| |
L2' U R2 U' L2 U R2' |
L1'-L2' U R1 U' L1-L2 U R1' |
L1'-L2' U R2 U' L1-L2 U R2' |
|
|
|
|
|
|
|
|
|
| |
L1' U R1-R2 U' L1 U R1'-R2' |
L2' U R1-R2 U' L2 U R1'-R2' |
L1'-L2' U R1-R2 U' L1-L2 U R1'-R2' |
|
|
|
2 remarques :
D'abord il est parfaitement inutile d'apprendre ces algorithmes par coeur. Il faut simplement comprendre leur mécanisme. Le principe est d'aligner sur la face avant et la face supérieure les cubes à échanger, avec la même disposition. On monte vers la face supérieure la ou les lignes de la face avant contenant le ou les cubes à échanger. Après un "Up", ces cubes se retrouvent à une nouvelle position. Il faut alors monter la ou les lignes de la face avant en regard de cette nouvelle position. Puis U'. On redescend ensuite la ou les lignes qu'on a monté en premier. Puis U. On redescend enfin la ou les lignes qu'on a monté en deuxième.
Deuxième remarque,
lorsque je déplace les lignes L1 ou R1, je déplace systématiquement avec elles les lignes L ou R, pour éviter des aller-retours inutiles. Mais pour simplifier l'écriture, je ne fais pas figurer ces mouvements dans les formules ci-dessus.
2. Appairer les arêtes :
Avec le cube 6x6, il y a 4 petits cubes à appairer sur chaque arête, 2 au milieu et 1 à chaque extrêmité. On n'a besoin d'aucune nouvelle formule, et on va se servir de ce qu'on a appris sur le 4x4 et le 5x5. Le principe est d'apparier en premier les 2 arêtes centrales et de positionner ensuite les arêtes latérales de chaque côté.
Pour apparier les arêtes centrales, j'utilise la technique du 4x4x4 : j'aligne 2 arêtes identiques face à face sur la ligne U2 ou D2 de la face antérieure, et je fais : [D-D1-D2] R F' U R' F [D'-D1'-D2'] (schéma n°9).
On peut alors considérer que cette arête n'est plus composée que par 3 cubes. On va pouvoir appliquer la technique du 5x5x5.
Je positionne la première arête latérale à côté de la centrale par [D-D1] R F' U R' F [D'-D1'] si l'arête se déplace sur la diagonale ascendante (schéma n°5), et par [U'-U1'] R F' U R' F [U-U1] pour la diagonale descendante (schéma n°7).
Puis je place la 2ème arête latérale avec :
- [D-D1] R F' U R' F [D'-D1'] : diagonale ascendante, arêtes centrales de droite à inverser, ou arêtes centrales de gauche OK (schéma n°5) ;
- [D-D1-D2-U2'] R F' U R' F [D'-D1'-D2'-U2] : diagonale ascendante, arêtes centrales de droite OK, ou arêtes centrales de gauche à inverser (schéma n°6) ;
- [U'-U1'] R F' U R' F [U-U1] : diagonale descendante, arêtes centrales de droite à inverser, ou arêtes centrales de gauche OK (schéma n°7) ;
- [U'-U1'-U2'-D2] R F' U R' F [U-U1-U2-D2'] : diagonale descendante, arêtes centrales de droite OK, ou arêtes centrales de gauche à inverser (schéma n°8).
Tous les autres cas vus au 5x5x5 sont également transposables.
Petit cas particulier : il peut arriver, par chance ou dans les dernières arêtes à appairer, qu'une arête latérale est déjà en place lorsqu'on veut appairer 2 arêtes centrales. Si j'applique la formule habituelle du schéma n°9, une des 2 arêtes latérales (celle qui est contre l'arête centrale déjà en place) reste à sa position, mais l'autre se déplace dans l'arête opposée. Par conséquent, pour appairer 2 arêtes centrales, si l'arête latérale juxtaposée à la position où l'arête centrale d'en face va venir est déjà bien placée, je fais alors :
- [D2] R F' U R' F [D2'] pour la diagonale ascendante (schéma n°1) ;
- [U2'] R F' U R' F [U2] pour la diagonale descendante (schéma n°3).
Pour aller un peu plus loin, s'il y a déjà 3 arêtes en place, et qu'il ne manque qu'une arête centrale à positionner on pourra utiliser d'autres variantes pour s'économiser des coups inutiles :
- [D2] R F' U R' F [D2'] : diagonale ascendante, arêtes latérales de droite à inverser, ou arêtes latérales de gauche OK (schéma n°1) ;
- [U2'] R F' U R' F [U2] : diagonale descendante, arêtes latérales de droite à inverser, ou arêtes latérales de gauche OK (schéma n°3) ;
- [U1'-D1-D2] R F' U R' F [U1-D1'-D2'] : diagonale ascendante, arêtes latérales de droite OK, ou arêtes latérales de gauche à inverser (schéma n°2) ;
- [U1'-U2'-D1] R F' U R' F [U1-U2-D1'] : diagonale descendante, arêtes latérales de droite OK, ou arêtes latérales de gauche à inverser (schéma n°4).
Chacun décidera suivant ses motivations de l'utilité d'encombrer sa mémoire avec ces variantes en sachant que le même résultat sera obtenu en utilisant plusieurs fois les formes de base. Économie de temps ou économie de mémoire ? C'est l'éternelle question... Quoi qu'il en soit, j'ai placé ci-dessous des schémas résumant les multiples situations en pratique :
|
|
|
|
|
|
|
[D2] R F' U R' F [D2'] |
[U1'-D1-D2] R F' U R' F [U1-D1'-D2'] |
[U2'] R F' U R' F [U2] |
[U1'-U2'-D1] R F' U R' F [U1-U2-D1'] |
|
|
|
|
|
|
|
[D1] R F' U R' F [D1'] |
[U2'-D1-D2] R F' U R' F [U2-D1'-D2'] |
[U1'] R F' U R' F [U1] |
[U1'-U2'-D2] R F' U R' F [U1-U2-D2'] |
|
|
|
|
|
|
|
[D1-D2] R F' U R' F [D1'-D2'] |
[U1'-U2'] R F' U R' F [U1-U2] |
[U2'-D2] R F' U R' F [U2-D2'] |
|
|
|
|
|
Même remarque que plus haut,
lorsque je déplace les lignes U1 ou D1, je déplace systématiquement avec elles les lignes U ou D, pour éviter des aller-retours inutiles. Mais pour simplifier l'écriture, je ne fais pas figurer ces mouvements dans les formules ci-dessus.
3. Refaire le cube comme un 3x3x3 :
Une fois que toutes les arêtes sont appairées, il ne reste plus qu'à recontruire le cube comme un vulgaire 3x3x3. Parfois, à la fin de l'étape précédente, il peut rester une dernière arête foireuse ; mais ce n'est pas grave, je recontruis malgré tout mon 3x3 en ne tenant compte que de la couleur des cubes latéraux de cette fameuse arête. Et je corrige le problème à l'étape de la croix jaune (voir ci-dessous).
4. Cas particuliers :
4.1. La dernière arête :
Il peut y avoir des ratés avec une arête. Trois cas de figure et leur solution :
|
|
|
|
| 4.1.1. |
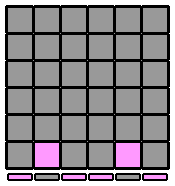 (vue antérieure)
(vue antérieure) |
L1 L1 B' B' D D R1 D D L1' D D L1 D D F F L1 F F R1' B' B' L1 L1 |
|
|
|
| 4.1.2. |
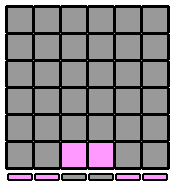 (vue antérieure)
(vue antérieure) |
L2 L2 B' B' D D R2 D D L2' D D L2 D D F F L2 F F R2' B' B' L2 L2 |
|
|
|
| 4.1.3. |
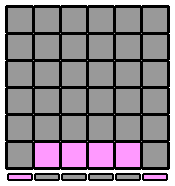 (vue antérieure)
(vue antérieure) |
L1-L2 L1-L2 B' B' D D R1-R2 D D L1'-L2' D D L1-L2 D D F F L1-L2 F F R1'-R2' B' B' L1-L2 L1-L2 |
|
|
|
Dans les 2 premiers cas ci-dessus, on s'aperçoit qu'il y a un souci dès la fin de la reconstruction des arêtes. Le 3ème cas est plus insidieux et ne se manifeste pas tout de suite. Quoi qu'il en soit, pour savoir ce qu'il y a de judicieux à faire, il faut attendre l'étape de la croix jaune du pseudo 3x3x3.
En effet, il y a 3 possibilités :
- s'il y a une arête visiblement foireuse et que je peux faire la croix jaune complète, alors je dois corriger cette arête par le cas 4.1.2 ;
- s'il y a une arête visiblement foireuse et que je ne peux faire la croix jaune (3 jaunes sur 4), alors je dois corriger cette arête par le cas 4.1.1 ;
- s'il y a pas d'arête foireuse en apparence, mais que je ne peux pas faire la croix jaune (3 jaunes sur 4), alors je retourne l'arête jaune mal orientée par le cas 4.1.3.
4.2. Deux coins à inverser :
|
|
|
| |
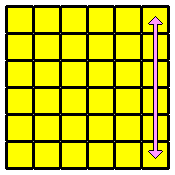 (vue inférieure)
(vue inférieure) |
C'est l'autre cas particulier, qu'on a déjà vu au cube 4x4x4 et qu'on résoudra en faisant :
[R D R' D' R' B R R D' R' D' R D R' B'] [F1-F2 F1-F2 D D F1-F2 F12 D-D1-D2 D-D1-D2 F1-F2 F1-F2 D1-D2 D1-D2] |
|
|
|
| Et voilà, vous avez fini ! |
 |
|
|
|
Avec cette méthode, et un peu d'entraînement, je mets une quinzaine de minutes pour refaire ce cube.
|
|
|
Quelques photos souvenirs :
|
|
|
 |
|
Un MoYu AoShi 6x6 (Stickerless Pink) de 2016. |
|
 |
|
 |
|
[L1 L1 R2' R2' R' R'] [F1 F1 B2' B2' B' B'] |
|
 |
|
Il est gentil, il fait des dessins... |
|
|
|
|