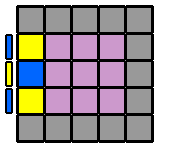
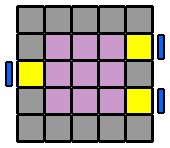
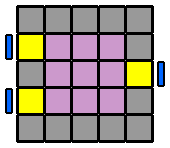
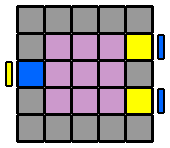
Comme pour le 4x4x4, j'utilise la méthode Hardwick pour résoudre le cube 5x5x5. Cependant, avec plus de cubes à placer, le cheminement jusqu'à l'équivalent de 3x3x3, sera un peu différent. Voyons ça de plus près...

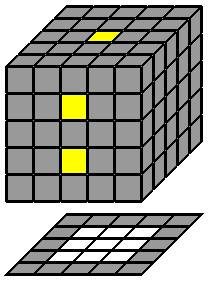
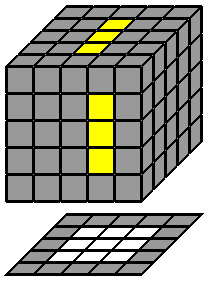
1. Faire le centre blanc :

Avec le 4x4x4, j'ai expliqué comment reconstruire les centres 2 par 2, mais cette façon de faire n'est pas intéressante ici, et ça sera un par un que je referai les centres de chaque face. Je commence comme d'habitude par le centre blanc en haut.
Je monte un petit cube blanc de chaque côté du centre blanc pour faire une ligne blanche horizontale de 3x1 sur la face supérieure (j'entends "horizontale" telle qu'elle se présente vue d'en haut, c'est à dire qu'elle se situe au niveau de la ligne coronale). Puis je pivote le cube de 90°dans l'axe des y pour que cette ligne soit verticale (toujours sur la face supérieure, vue d'en d'haut, c'est à dire au niveau de la ligne médiane). Ensuite, je construis une ligne blanche, verticale, de 1x3 sur la face avant, et je la monte à la face supérieure. Je répète la même chose pour la 3ème ligne verticale. Le centre blanc est terminé. Il n'y a pas de difficulté particulière à cette étape, puisque rien n'est encore construit par ailleurs.


2. Faire le centre jaune :

Je retourne maintenant le cube de 180° pour placer le centre jaune en haut, et je vais reproduire exactement la même démarche que précédemment, sauf qu'il faudra se préoccuper de ne pas défaire le centre blanc déjà créé.

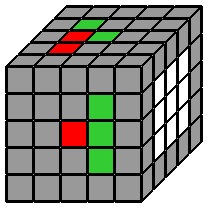
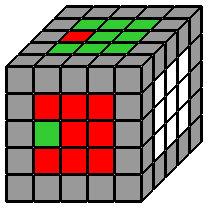
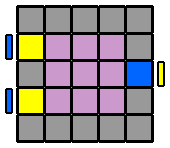
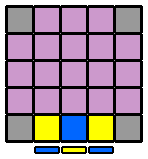
3. Faire le centre bleu :

Je pivote ensuite le cube de 90° sur l'axe des z, pour placer le centre bleu en haut et le blanc à droite. Je reconstruis alors le centre bleu un peu comme je l'ai fait pour le centre blanc. Je place un petit cube bleu de chaque coté du centre bleu pour former une ligne "horizontale" bleue de 3x1 et je la "verticalise" par U ou U'. Puis je monte successivement les 2 autres lignes verticales que j'aurai créées au préalable sur la face orange, rouge ou verte. Je n'ai pas à me soucier de défaire les faces blanche et jaune, puisque je n'ai besoin de faire aucun mouvement qui risque de les détruire.

Encore une fois, vous êtes libres de reconstruire à cette étape une autre couleur que la bleue, ou de placer la face jaune sur la droite si cela vous chante, dans la mesure où les centres sont fixes, on ne peut pas se tromper sur la disposition relative des différentes couleurs. Cependant, c'est l'ordre dans lequel j'ai l'habitude de procéder et avoir des automatismes me permet d'avancer bien plus vite.


4. Faire le centre orange :

Je m'attaque ensuite au centre orange, avec la méthode qui m'a servi pour le centre jaune, en prenant soin de ne pas défaire le bleu.


5. Faire les centres vert et rouge :

Les 2 derniers centres sont un peu plus compliqués à faire.

En utilisant plusieurs fois successives la methode ci-dessus ou sa forme en miroir, il ne reste que quelques rares cubes mal positionnés, qu'on échangera un par un avec un des 2 algorithmes ci-dessous :

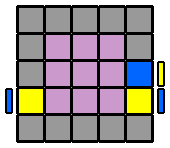
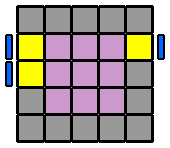
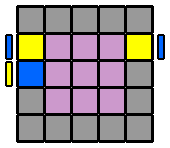
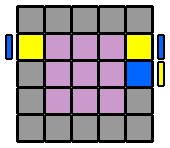
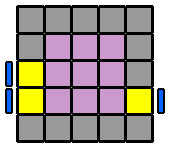
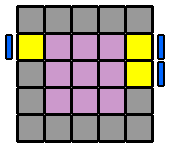
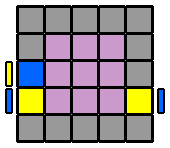
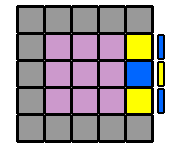
6. Appairer les arêtes :

Pour former les arêtes, je reprends le même algorithme que pour le 4x4x4. Cependant, suivant la ou les étages qu'on va envoyer à droite en début d'algorithme, on va se constituer des variantes qui permettront de résoudre tous les différents cas de figure.

Je repère d'abord une arête centrale et une arête latérale de la même couleur et je les place en vis à vis sur la face avant, sans me soucier de leurs orientations respectives. Si l'arête latérale, pour venir auprès de l'arête centrale, se déplace sur la diagonale ascendante (ligne qui va du coin inférieur gauche au coin supérieur droit, dans un sens comme dans l'autre), je commence l'algorithme par l'étage du bas ([6.1.]). Si elle se déplace sur la diagonale descendante (coin supérieur gauche à inférieur droit, dans un sens ou l'autre), alors c'est l'étage du haut que j'envoie vers la droite au début de l'algorithme ([6.3.]). Puis, je place la 2ème arête latérale à l'avant, en face de la première arête latérale déjà appairée, et avec la même orientation que celle-ci. De la même façon, suivant la diagonale ascendante ou descendante que devra prendre cette nouvelle arête pour rejoindre les 2 autres, j'enverrai sur la droite l'étage du bas ou du haut. Mais si l'arête centrale de droite à la même orientation ou celle de gauche a une orientation inversée par rapport aux 2 latérales, j'englobe aussi la ligne équatoriale ([6.2.] et [6.4.]). Le détail en images...

C'est finalement beaucoup plus simple que ces nombreux schémas pourraient le laisser croire. Cependant, si vous êtes allergiques à cette petite gymnastique intellectuelle, vous pourrez malgré tout traverser cette étape avec succès, puisque toutes les arêtes peuvent être résolues en utilisant uniquement le cas de gauche des points [6.1.] et [6.2.]. Mais pour arriver à cette configuration (les arêtes latérales appariées en bas et l'arête centrale à droite) cela oblige à faire des mouvements inutiles qui vous feront perdre du temps. Chacun trouvera sa voie suivant ses besoins.

Ainsi, vous aurez 12 arêtes à appairer avant d'avoir votre équivalent de 3x3x3, sauf si...

6.8. Un seul cas particulier :

7. Refaire le cube comme un 3x3x3 :

Avec cette méthode, je mets environ 8 minutes pour refaire ce cube. On est bien loin des performances des champions qui ne dépassent pas la minute. Je me justifierai fallacieusement en disant que je préfère savourer et prendre mon temps...