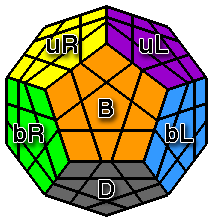
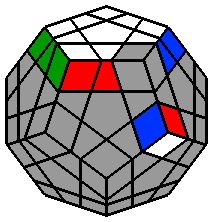
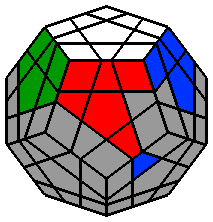
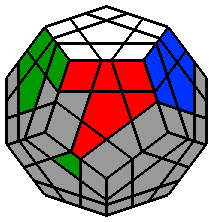
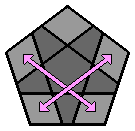
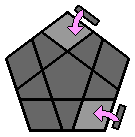
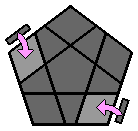
Le Mégaminx est un dodécaèdre régulier. Il se compose de 12 faces pentagonales, chacune d'entre elles étant constituée de 11 pièces : 1 centre, 5 arêtes et 5 coins.

Ce casse-tête est beaucoup plus simple qu'il en a l'air et s'apparente à un classique 3x3x3 dont on va pouvoir adapter la méthodologie et les algorithmes.
Si vous êtes familiers du 3x3x3, vous allez l'adorer !

Concernant la notation conventionnelle des mouvements, chaque face est désignée par une abréviation :

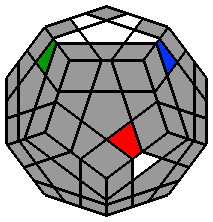
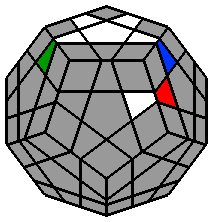
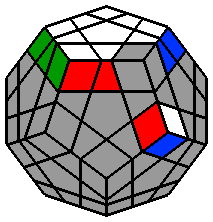
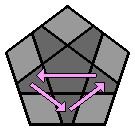
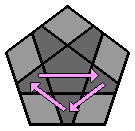
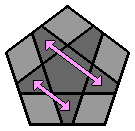
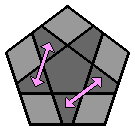
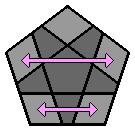
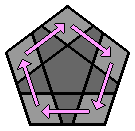
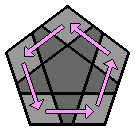
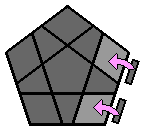
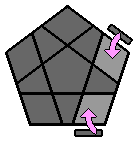
Chaque lettre majuscule correspond dans les formules à une rotation de la face concernée d'1/5 de tour dans le sens des aiguilles d'une montre, lorsque cette face est orientée vers l'observateur. Si un ' accompagne la lettre majuscule, la rotation se fait alors dans le sens inverse des aiguilles d'une montre.


1. Faire l'étoile blanche à la face supérieure :

Comme pour le 3x3x3, je commence par placer les arêtes de la face supérieure. J'ai l'habitude de débuter par la face blanche, mais chacun est libre de commencer ailleurs.
Il n'y a pas de façon de faire uniforme, le plus souvent, je positionne l'arête blanche au niveau de la face avant.

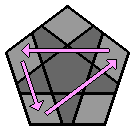
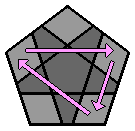
2. Positionner les coins blancs :

Je dispose ensuite les 5 coins blancs, un par un, entre les branches de l'étoile blanche.
Pour cela, je place le coin au pied de sa future place, si possible j'évite que le blanc regarde vers le bas. Et je l'insère à la face supérieure avec une méthode inspirée du 3x3x3 :

3. Faire la 2ème couronne :

On utilise ici la même méthode que pour le 3x3x3, surnommée "le Belge" :

Pour positionner l'arête à placer, il est souvent intéressant de la faire transiter par la face inférieure. C'est plus rapide.


4. Faire la face jaune et sa 2ème couronne :

Une fois qu'on a terminé la 2ème couronne de la face blanche, on peut terminer les étages inférieurs (à part la face inférieure) comme un 3x3x3, par couches successives. Au début, j'avais l'habitude de recontruire en premier les 5 triplets de 3 pièces consécutives formant la partie supérieure de la ligne équatoriale (c'est-à-dire toutes les pièces du zig-zag équatorial sauf les coins les plus inférieurs). Je positionnais l'arête de gauche du triplet par simple déplacement, puis le coin supérieur qui est juste adjacent à sa droite avec la méthode ci-dessus (point 2.) et je plaçais l'arête restante du triplet (juste à la droite du coin supérieur) par un Belge (point 3.). Il ne me restait plus qu'à positionner tous les coins équatoriaux inférieurs qui ne sont pas gris, et enfin les arêtes de l'avant-dernier étage (on repère rapidement celles qui ne sont pas grises). Mais avec le temps, je préfère maintenant utiliser une autre méthode, en reconstruisant le Mégaminx "face par face". Je trouve qu'on se disperse moins, et le repérage est plus simple. C'est donc la technique que je décrirai ci-dessous. Notez que ces 2 méthodes sont équivalentes, avec le même nombre de Belges nécessaires. Mais pour la 2ème méthode, je reconstruis directement l'avant-dernière couronne sans attendre d'avoir terminé le zig-zag équatorial.

Donc... après la face blanche initiale, il faut reconstruire une face adjacente. J'ai l'habitude de faire la jaune, puisque les pièces jaunes, plus claires, se repèrent facilement.
En premier lieu je positionne les 2 arêtes jaunes restantes par simple déplacement. Puis j'insère les 3 coins jaunes restants par la méthode du point 2. Ensuite je termine la 2ème couronne de la face jaune en insérant les 3 arêtes (bleu marine-vert-orange-violet) par simples Belges.


5. Faire la face violette et sa 2ème couronne :

Après la face jaune, il faut reconstruire la face adjacente à la blanche, se situant à droite de la jaune, à savoir, la violette. De la même façon que précédemment avec la face jaune, je place l'arête violette restante, puis les 2 derniers coins violets, puis les 2 arêtes de sa 2ème couronne (orange-bleu-vert foncé).


6. Finir les autres faces et leur 2ème couronne :

Toujours sur le même principe que précédemment, je termine la face à droite de la précédente (toujours adjacente à la blanche), c'est à dire la face vert foncé et sa 2ème couronne. Puis je recontruis la face rouge (à droite de la vert foncé) et sa 2ème couronne ; mais désormais je dois faire attention de ne pas défaire les cubes bleu marine bien placés au début. Il faut pour cela transiter par la face inférieure. Puis on finit le dernier coin bleu et l'arête rose-vert par un Belge.

Il ne reste plus que la face inférieure à finir !


7. Faire une étoile grise :

Toujours sur le modèle du 3x3x3, je commence par orienter les arêtes de la face inférieure dans le bon sens :

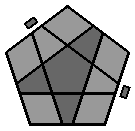
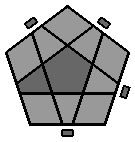
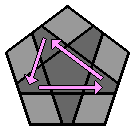
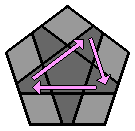
8. Orienter l'étoile grise :

Puis on fait correspondre l'étoile grise avec les couleurs des faces adjacentes :

On remarquera que finalement, tous les cas de figure possibles à cette étape peuvent se résoudre en utilisant uniquement les cas [8.1] et [8.3]. Il n'est donc pas indispensable d'encombrer sa mémoire avec toutes ces éventualités et leurs solutions. Cependant, avec un peu d'habitude, vous verrez que c'est un effort qui n'est pas si laborieux au regard du temps que cela fait gagner.


9. Positionner les coins :

Ensuite on place les coins du dernier étage à leur bonne position, sans se soucier de leur orientation :

S'il y a déjà 2 coins adjacents bien placés, un de ces 2 algorithmes suffira à finaliser cette étape.
S'il n'y a qu'un seul coin bien placé, il faudra positionner un 2ème cube à côté de ce dernier à l'aide d'un de ces 2 algorithmes, puis réutiliser un de ces 2 algorithmes pour finaliser le positionnement des coins.
Et s'il n'y a aucun coin bien placé, on en positionne un, puis un 2ème adjacent, puis on les termine tous.
Ainsi, en utilisant au maximum 3 fois cet algorithme, on place correctement tous les coins quelle que soit la configuration initiale.

Quelques cas particuliers peuvent cependant être utiles à ceux qui n'ont pas peur d'embarrasser leur mémoire :

10. Orienter les coins :

Enfin, on fait descendre les faces grises des coins mal orientés, et le casse-tête est terminé :

Avec cette méthode, je mets environ 8 minutes pour résoudre le Mégaminx.