On va commencer par le petit de la famille... Voici, étape par étape, la méthode que j'utilise pour résoudre le cube 2x2x2.

Pour plus de clarté, et malgré mon aversion pour l'impérialisme linguistique de l'anglais, je me servirai de la notation conventionnelle internationale pour expliciter les mouvements du cube. À savoir :

- R = la face de droite (right), orientée vers l'observateur, fait un quart de tour dans le sens des aiguilles d'une montre ;
- R' = la face de droite (right), orientée vers l'observateur, fait un quart de tour dans le sens inverse des aiguilles d'une montre ;

- L = la face de gauche (left), orientée vers l'observateur, fait un quart de tour dans le sens des aiguilles d'une montre ;
- L' = la face de gauche (left), orientée vers l'observateur, fait un quart de tour dans le sens inverse des aiguilles d'une montre ;

- U = la face supérieure (up), orientée vers l'observateur, fait un quart de tour dans le sens des aiguilles d'une montre ;
- U' = la face supérieure (up), orientée vers l'observateur, fait un quart de tour dans le sens inverse des aiguilles d'une montre ;

- D = la face inférieure (down), orientée vers l'observateur, fait un quart de tour dans le sens des aiguilles d'une montre ;
- D' = la face inférieure (down), orientée vers l'observateur, fait un quart de tour dans le sens inverse des aiguilles d'une montre ;

- F = la face avant (front), orientée vers l'observateur, fait un quart de tour dans le sens des aiguilles d'une montre ;
- F' = la face avant (front), orientée vers l'observateur, fait un quart de tour dans le sens inverse des aiguilles d'une montre ;

- B = la face arrière (back), orientée vers l'observateur, fait un quart de tour dans le sens des aiguilles d'une montre ;
- B' = la face arrière (back), orientée vers l'observateur, fait un quart de tour dans le sens inverse des aiguilles d'une montre.

1. Recontruire le premier étage :

Mélangez votre cube. Lâchez-vous, dans tous les sens. Laissez aller votre créativité. Maintenant, la première tâche qui vous attend, est de refaire la face du haut et sa couronne.

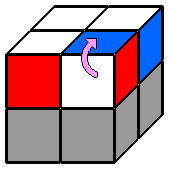
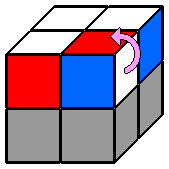
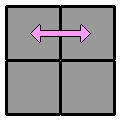
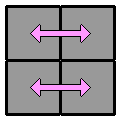
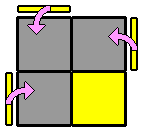
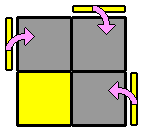
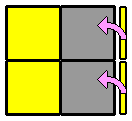
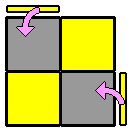
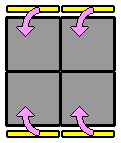
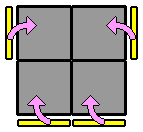
Par habitude, je commence toujours par la face blanche en haut. D'abord parce que les cubes blancs, plus clairs, se repèrent facilement. Ensuite, parce que débuter systématiquement par la même face permet de connaître facilement la disposition des autres couleurs tout autour. On gagne du temps.

Cette première étape ne présente pas de difficulté particulière. On désigne comme face supérieure une face qui contient déjà une cube blanc. Puis on place, un par un, les 3 autres coins blancs en faisant attention de bien faire correspondre la couleur des faces latérales. Lorsque plusieurs cubes blancs sont bien placés, pour en positionner un nouveau sans défaire les précédents, on peut s'aider d'une des techniques ci-dessous, ou de leur forme en miroir :

Remarquez que dans les 3 derniers exemples, il s'agit juste de replacer le coin mal positionné pour retomber dans un des 2 premiers cas de figure.


2. Positionner les coins de l'étage inférieur :

On va maintenant s'attaquer à l'étage du bas en positionnant chaque coin à sa future place. Il n'y a qu'un seul algorithme à connaître, qui permet d'échanger les 2 coins de la face avant et de résoudre tous les cas de figure de cette étape.

Pour la procédure, il faut d'abord repérer à l'étage inférieur 2 coins adjacents qui possèdent une couleur commune (hormis la jaune) et les aligner sur la face avant avec les coins de la face supérieure qui ont cette couleur. Cela permet d'un coup d'oeil de voir si ces 2 coins inférieurs sont bien placés (dans ce cas, une de leurs 3 couleurs correspond à la face latérale adjacente), ou s'ils doivent être échangés (ils n'ont pas la couleur de la face latérale adjacente). On repère ensuite la même chose avec les 2 coins arrière.

Il y a donc 4 possibilités qui se présentent quand on vient de finir l'étape de la première couronne :

2.1. Les 4 coins inférieurs sont déjà bien placés. Vous avez de la chance, vous pouvez passer directement à l'étape 3.

2.2. Seuls les 2 coins avant de la face inférieure sont mal placés. On va les intervertir à l'aide de la formule suivante (qu'on va appeler [2R] par commodité) :

2.3. Seuls les 2 coins arrière de la face inférieure sont mal placés. Il suffit de retourner le cube en entier de 180° pour placer la face arrière à l'avant et on utilise la formule précédente (qui intervertit les coins inférieurs-avant).

2.4. Les 4 coins inférieurs sont mal placés. On devra appliquer la formule [2R] successivement sur la face avant puis sur la face arrière. Ce qui en pratique revient à faire, compte tenu du déplacement des doigts :

3. Orienter les coins de l'étage inférieur :

Dernière ligne droite...tous les cubes sont en place, il ne reste plus qu'à les faire pivoter sur eux-mêmes pour que le casse-tête soit terminé.
À cette étape, il n'y a que 8 cas de figure possibles et un seul algorithme à connaître pour faire descendre les 4 jaunes à la face inférieure.

L'algorithme est le suivant : R' D D R D R' D R (que l'on appellera [3R]).
Mais il faut connaître aussi sa version miroir : L D' D' L' D' L D' L' (que l'on appellera [3L]).

Suivant chacun des cas de figures, l'algorithme s'appliquera d'une manière différente :

3.1. Les 4 jaunes sont sur la face inférieure. Bon sang, mais c'est votre jour de chance ! Le cube est déjà fini et vous n'avez rien eu à faire...

3.2. Un seul jaune se trouve sur la face inférieure. Deux éventualités, et leur solution, dont le sens d'exécution est donné par le côté du jaune latéral le plus proche du jaune inférieur :

3.3. Deux jaunes se trouvent sur la face inférieure. Trois éventualités, que l'on résoudra avec une seule méthode :

3.4. Aucun jaune ne se trouve sur la face inférieure. Deux éventualités suivant l'orientation des jaunes sur les faces latérales... et leurs solutions :

[NB] : Pour ceux qui ne sont pas pressés, et qui n'ont pas envie d'encombrer leur mémoire, je ferai remarquer que tous les cas de figure de l'étape 3 peuvent être résolus en appliquant uniquement la formule [3R] + [3L] judicieusement et au maximum 2 fois d'affilée. C'est d'ailleurs cette méthode que j'utilise pour le cube 3x3x3, et que je détaille sur la page dédiée.

Pour faire le cube avec cette méthode, il faut environ 30 à 50 mouvements, ce qui prend entre 10 et 15 secondes avec de l'entrainement. Ce n'est pas la seule et unique façon de faire. Il existe de nombreuses variantes que je vous laisse éprouver. Certaines sont plus rapides mais nécessitent un effort de mémoire et un entrainement plus conséquent. La mienne a l'avantage d'être facilement accessible et reproductible sur les cubes plus gros. Je vous invite d'ailleurs à visiter les autres pages de ce site pour vous en faire une idée...