|
Le Square-1 est un cube difficile qui mélange à la fois formes et couleurs, avec une logique qui ne correspond à aucun autre cube précédent (3x3, Dino, Skewb...). Quand on s'amuse avec, on se rend rapidement compte qu'il est trop complexe de trouver des algorithmes qui corrigent en même temps sa forme et ses couleurs. Pour le résoudre, il faut d'abord lui redonner son apparence cubique symétrique, puis on pourra réorganiser ses couleurs en échangeant les pièces de place.
La notation conventionnelle que j'utiliserai dans les algorithmes ci-dessous est particulière.
|
|
|
|
Tout d'abord j'ai pris l'habitude de toujours tenir le Square-1 avec le petit côté rouge de la couronne intermédiaire sur la gauche de la face avant (voir ci-contre), quelle que soit l'orientation des autres pièces.
Par ailleurs, chaque formule est une succession de barres obliques / (slash) séparant des séries de 2 chiffres.
Chaque slash
correspond à une rotation d'un demi-tour de la partie droite du Square-1 (schéma de gauche).
Pour pouvoir faire cette rotation, il faut donc faire correspondre un plan de section sur les faces supérieure et inférieure passant juste à droite de la petite pièce rouge de la 2ème couronne.
|
|
|
|
|
En ce qui concerne les chiffres, le premier chiffre de chaque série correspond à une rotation de la face supérieure et le deuxième à une rotation de la face inférieure.
La valeur du chiffre donne l'indication de la quantité de rotation, en sachant que la valeur 1 est égale à la largeur d'un autocollant de la couronne de la face supérieure ou inférieure (les verticaux).
Pour des valeurs positives, le sens de rotation sera horaire (face orientée vers l'observateur), et à l'inverse anti-horaire pour les chiffres négatifs (voir schéma ci-contre à gauche).
Par exemple
une formule indiquant / 3 -1 / -2 0 / correspond à :
-
demi-tour de la moitié de droite ;
- rotation de la face supérieure, dans le sens des aiguilles d'une montre, de 3 autocollants
latéraux ;
- rotation de la face inférieure, dans le sens inverse des aiguilles d'une montre, d'un autocollant
latéral ;
-
demi-tour de la moitié de droite ;
- rotation de la face supérieure, dans le sens inverse des aiguilles d'une montre, de 2 autocollants
latéraux ;
- pas de rotation de la face inférieure ;
-
demi-tour de la moitié de droite.
|
|
|
|
|
|
|
1. Redonner une forme cubique :
Les faces supérieure et inférieure se composent de 2 sortes de pièces : les coins, en forme de losange, et les arêtes, de forme triangulaire. Il y a en tout 8 coins et 8 arêtes, répartis sur ces 2 faces.
La première étape pour que le Square-1 retrouve sa forme cubique, consiste à aligner 6 arêtes consécutives à l'étage du haut, à gauche de la ligne de section. Il n'y a pas de méthode particulière, c'est assez simple avec un petit peu de réflexion. Je place les arêtes déjà sur la face supérieure juste à gauche de la ligne de section. J'en trouve d'autres sur la face inférieure que je place juste à droite de la ligne de section. Et avec un "slash", les 2 groupes d'arêtes sont côte à côte à la face supérieure. Je pivote l'ensemble à gauche de la ligne de section et je continue à monter ainsi d'autres arêtes à la face supérieure jusqu'à en obtenir 6 d'affilée.
Deuxième étape, après 6 arêtes consécutives, je dois aligner les 2 dernières avec les précédentes.
Je place ces 2 arêtes
restantes sur la face inférieure. Et j'exécute l'algorithme approprié suivant le cas de figure sur les 3 éventualités possibles :
|
|
|
| |
1.1. |
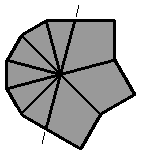 (vue supérieure)
(vue supérieure) |
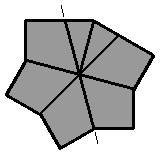 (vue inférieure)
(vue inférieure) |
|
Les 2 arêtes de la face inférieure sont consécutives, il suffit de faire :
[ / ] |
|
|
|
| |
1.2. |
 (vue supérieure)
(vue supérieure) |
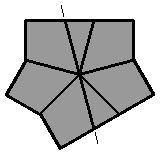 (vue inférieure)
(vue inférieure) |
|
Les 2 arêtes de la face inférieure sont face à face, on fait :
[ / ] |
|
|
|
| |
1.3. |
 (vue supérieure)
(vue supérieure) |
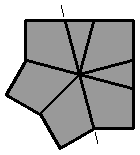 (vue inférieure)
(vue inférieure) |
|
Les 2 arêtes de la face inférieure sont séparées par un coin :
[ 2 0 / 3 -2 / 0 2 / ] |
|
|
|
Maintenant que les 8 arêtes sont alignées, on peut redonner au Square-1 sa forme cubique grâce à l'algorithme ci-dessous :
|
|
|
| |
1.4. |
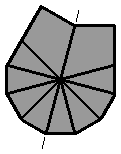 (vue supérieure)
(vue supérieure) |
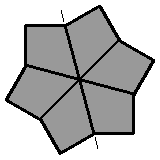 (vue inférieure)
(vue inférieure) |
|
[ / -2 -4 / -1 -2 / -3 -3 / ] |
|
|
|
Il se peut que la 2ème couronne ne soit pas correctement placée. On peut, si on le souhaite, la corriger en faisant [ / 6 0 / 6 0 / ]. Mais en pratique, cela n'a pas d'importance à ce stade, d'autant que l'étape suivante l'inverse souvent à nouveau.
2. Positionner les coins :
2.1. Placer le coin blanc-rouge-vert en haut à gauche de la face supérieure :
Je positionne tout d'abord la pièce blanc-rouge-vert au niveau du coin supérieur arrière gauche.
Si cette pièce est déjà sur la face supérieure, il suffit de faire tourner la première couronne pour positionner la pièce.
Si cette pièce est au niveau de l'étage inférieur, il suffit de la positionner sur l'un des 2 coins à droite de la ligne de section et on la déplace sur la face supérieure en faisant [ 1 0 / ]. Puis on pivote la face supérieure comme précédemment pour placer la pièce sur le bon angle.
2.2. Placer le coin blanc-orange-vert en haut à droite de la face supérieure :
On va se servir de la même méthode que précédemment pour monter la pièce blanc-orange-vert sur l'angle supérieur arrière droit, à côté de la blanc-rouge-vert. Puis on fait [ -3 0 ] pour conserver ces 2 coins à gauche de la ligne de section.
En pratique, il est plus rapide de repérer la position initiale de ces 2 coins blanc-vert pour les placer correctement en un minimum de coups. Par exemple, si à l'étape [2.1] le coin blanc-orange-vert est déjà sur la face supérieure, mais pas le coin blanc-rouge-vert, on montera directement ce dernier à sa bonne position (relative au blanc-orange-vert) en choisissant la bonne rotation.
2.3. Placer le coin blanc-rouge-bleu en haut à droite de la face supérieure et le blanc-orange-bleu en haut à gauche de la face inférieure :
Puis on fait [ 1 0 / 0 3 / (-1 0) ]. Tous les coins de la face supérieure sont bien placés et ceux de la face inférieure bien orientés. Par ailleurs, c'est maintentant que je corrige la deuxième couronne
lorsque c'est nécessaire.
2.4. Positionner les coins jaunes :
Si besoin, on permutera les coins de la face inférieure. Deux cas de figure :
|
|
|
| |
2.4.1. |
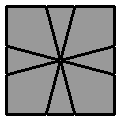 (vue supérieure)
(vue supérieure) |
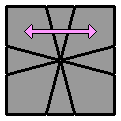 (vue inférieure)
(vue inférieure) |
|
[ / 3 -3 / 0 3 / -3 0 / 3 0 / -3 0 / (0 3) ] |
|
|
|
| |
2.4.2. |
 (vue supérieure)
(vue supérieure) |
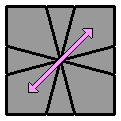 (vue inférieure)
(vue inférieure) |
|
[ / 3 3 / 0 3 / 3 3 / 0 3 / 3 3 / (0 3) ]
On peut aussi faire [2.4.1] + [2.4.1 face arrière (bas)], c'est à dire :
[ / 3 -3 / 0 3 / -3 0 / 3 0 / -3 0 / 0 -3 ] [ / 3 -3 / 0 3 / -3 0 / 3 0 / -3 0 / 0 6 ] |
|
|
|
3. Orienter les centres :
On va maintenant mettre tous les blancs en haut et tous les jaunes en bas. Je dégrossis la tâche avec le premier algorithme ci-dessous, qui est rapide. Puis je termine avec le deuxième, qui est plus long mais permet de gérer toutes les éventualités.
|
|
|
| |
3.1. |
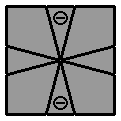 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[ 1 0 / -1 -1 / (0 1) ] |
|
|
|
| |
3.2. |
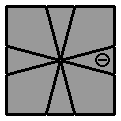 (vue supérieure)
(vue supérieure) |
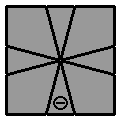 (vue inférieure)
(vue inférieure) |
|
[ 1 0 / 3 0 / 3 0 / -1 -1 / -2 1 / -3 0 / (-1 0) ] |
|
|
|
4. Positionner les centres :
Il ne reste plus qu'à permuter les centres entre eux pour terminer le cube. On piochera l'algorithme dont on a besoin ci-dessous :
|
|
|
| |
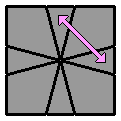
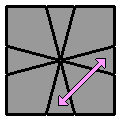
4.1. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[ -2 0 / 3 0 / -1 -1 / -2 1 / (2 0) ] |
|
|
|
| |
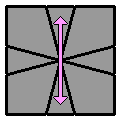
4.2. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[3.1] + [3.1 face arrière (bas)]
[ 1 0 / -1 -1 / 0 -5 ] [ 1 0 / -1 -1 / 0 -5 ] |
|
|
|
| |
4.3. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[ / -3 0 / 0 3 / 0 -3 / 0 3 / 2 0 / 0 2 / -2 0 / 4 0 / 0 -2 / 0 2 / -1 4 / 0 -3 / 0 3 ] [ / 6 0 / 6 0 / 6 0 ] |
|
|
|
| |
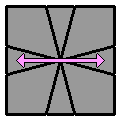
4.4. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[ / 3 3 / -1 0 / 2 -4 / 4 -2 / 0 -2 / -4 2 / 1 -5 / 3 0 / 3 3 / 3 0 ] |
|
|
|
| |
4.5. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[4.1] + [4.1 face de droite (haut)]
[ -2 0 / 3 0 / -1 -1 / -2 1 / 5 0 ] [ -2 0 / 3 0 / -1 -1 / -2 1 / -1 0 ] |
|
|
|
| |
4.6. |
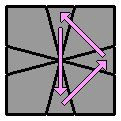 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[4.1] + [4.1 face de gauche (haut)]
[ -2 0 / 3 0 / -1 -1 / -2 1 / -1 0 ] [ -2 0 / 3 0 / -1 -1 / -2 1 / 5 0 ] |
|
|
|
| |
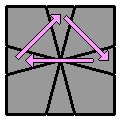
4.7. |
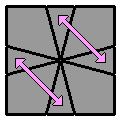 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[4.1] + [4.1 face arrière (haut)]
[ -2 0 / 3 0 / -1 -1 / -2 1 / -4 0 ] [ -2 0 / 3 0 / -1 -1 / -2 1 / -4 0 ] |
|
|
|
| |
4.8. |
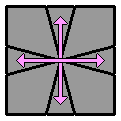 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[4.2] + [4.2 face de droite (haut)] (= [4.2] + [4.2 face de gauche (haut)])
[ 1 0 / -1 -1 / 0 -5 ] [ 1 0 / -1 -1 / 0 -5 ] [ 3 0 ] [ 1 0 / -1 -1 / 0 -5 ] [ 1 0 / -1 -1 / 0 -5 ] [ -3 0 ] |
|
|
|
| |
4.9. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[4.1] + [4.1 face de droite (bas)]
[ -2 0 / 3 0 / -1 -1 / -2 1 / 2 -3 ] [ -2 0 / 3 0 / -1 -1 / -2 1 / 2 3 ] |
|
|
|
| |
4.9. |
 (vue supérieure)
(vue supérieure) |
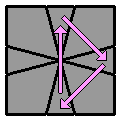 (vue inférieure)
(vue inférieure) |
|
[4.1] + [4.1 face de gauche (bas)]
[ -2 0 / 3 0 / -1 -1 / -2 1 / 2 3 ] [ -2 0 / 3 0 / -1 -1 / -2 1 / 2 -3 ] |
|
|
|
| |
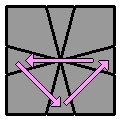
4.9. |
 (vue supérieure)
(vue supérieure) |
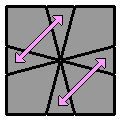 (vue inférieure)
(vue inférieure) |
|
[4.1] + [4.1 face arrière (bas)]
[ -2 0 / 3 0 / -1 -1 / -2 1 / 2 -6 ] [ -2 0 / 3 0 / -1 -1 / -2 1 / 2 -6 ] |
|
|
|
| |
4.9. |
 (vue supérieure)
(vue supérieure) |
 (vue inférieure)
(vue inférieure) |
|
[4.2] + [4.2 face de droite (bas)] (= [4.2] + [4.2 face de gauche (bas)])
[ 1 0 / -1 -1 / 0 -5 ] [ 1 0 / -1 -1 / 0 -5 ] [ 0 3 ] [ 1 0 / -1 -1 / 0 -5 ] [ 1 0 / -1 -1 / 0 -5 ] [ 0 -3 ] |
|
|
|
5. Si besoin :
Permuter la 2ème couronne : [ / 6 0 / 6 0 / 6 0 ]
Inverser les faces jaunes et blanches : [ / -6 -6 / -1 -1 ] ou [ 1 0 / 6 6 / -1 0 ]
|
|
|
| Et voilà, c'est terminé ! |
 |
|
|
|
Avec cette méthode, il me faut environ 3 minutes en moyenne pour reconstruire ce cube.
|
|
|
Quelques photos souvenirs :
|
|
|
 |
|
Calvin's Square-1 (Blanc) de 2015. |
|
 |
|
 |
|
QiYi Square-1 (Stickerless) de 2016. |
|
 |
|
|
|